Space & Physics

Why does superconductivity matter?

Published

12 months ago

February 17, 2024

A high-temperature (liquid nitrogen cooled) superconductor levitating above a permanent magnet (TU Dresden). Credit: Henry Mühlpfordt/Wikemedia Commons

Superconductivity was discovered by H. Kamerlingh Onnes on April 8, 1911, who was studying the resistance of solid Mercury (Hg) at cryogenic temperatures. Liquid helium was recently discovered at that time. At T = 4.2K, the resistance of Hg disappeared abruptly. This marked a transition to a new phase that was never seen before. The state is resistanceless, strongly diamagnetic, and denotes a new state of matter. K. Onnes sent two reports to KNAW (the local journal of the Netherlands), where he preferred calling the zero-resistance state ‘superconductivity’’.

There was another discovery that went unnoticed in the same experiment, which was the transition of superfluid Helium (He) at 2.2K, the so-called λ transition, below which He becomes a superfluid. However, we shall skip that discussion for now. A couple of years later, superconductivity was found in lead (Pb) at 7K. Much later, in 1941, Niobium Nitride was found to superconduct below 16 K. The burning question in those days was: what would the conductivity or resistivity of metals be at a very low temperature?

The reason behind such a question is Lord Kelvin’s suggestion that for metals, initially the resistivity decreases with falling temperature and finally climbs to infinity at zero Kelvin because electrons’ mobility becomes zero at 0 K, yielding zero conductivity and hence infinite resistivity. Kamerlingh Onnes and his assistant Jacob Clay studied the resistance of gold (Au) and platinum (Pt) down to T = 14K. There was a linear decrease in resistance until 14 K; however, lower temperatures cannot be accessed owing to the unavailability of liquid He, which eventually happened in 1908.

*Heike Kamerlingh Onnes (right), the discoverer of superconductivity. Paul Ehrenfest, Hendrik Lorentz, Niels Bohr stand to his left.*

In fact, the experiment with Au and Pt was repeated after 1908. For Pt, the resistivity became constant after 4.2K, while Au is found to superconduct at very low temperatures. Thus, Lord Kelvin’s notion about infinite resistivity at very low temperatures was incorrect. Onnes had found that at 3 K (below the transition), the normalised resistance is about 10⁻⁷. Above 4.2 K, the resistivity starts appearing again. The transition is too sharp and falls abruptly to zero within a temperature window of 10⁻⁴ K.

Perfect conductors, superconductors, and magnets

All superconductors are normal metals above the transition temperature. If we ask in the periodic table where most of the superconductors are located, the answer throws some surprises. The good metals are rarely superconducting. The examples are Ag, Au, Cu, Cs, etc., which have transition temperatures of the order of ∼ 0.1K, while the bad metals, such as niobium alloys, copper oxides, and 1 MgB2, have relatively larger transition temperatures. Thus, bad metals are, in general, good superconductors. An important quantity in this regard is the mean free path of the electrons. The mean free path is of the order of a few A⁰for metals (above T_c), while for good metals (or the bad superconductors), it is usually a few hundred of A⁰. Whereas for the bad metals (good superconductors), it is still small as the electrons are strongly coupled to phonons. The orbital overlap is large in a superconductor. In good metals, the orbital overlap is small, and often they become good magnets. In the periodic table, transition elements such as the 3D series elements, namely Al, Bi, Cd, Ga, etc., become good superconductors, while Cr, Mn, and Fe are bad superconductors and in fact form good magnets. For all of them, that is, whether they are superconductors or magnets, there is a large density of states at the Fermi level. So, a lot of electronic states are necessary for the electrons in these systems to be able to condense into a superconducting state (or even a magnetic state). The nature of the electronic wave function determines whether they develop superconducting order or magnetic order. For example, electronic wavefunctions have a large spatial extent for superconductors, while they are short-range for magnets.

Meissner effect

The near-complete expulsion of the magnetic field from a superconducting specimen is called the Meissner effect. In the presence of a magnetic field, the current loops at the periphery will be generated so as to block the entry of the external field inside the specimen. If a magnetic field is allowed within a superconductor, then, by Ampere’s law, there will be normal current within the sample. However, there is no normal current inside the specimen. Thus, there can’t be any magnetic field. For this reason, superconductors are known as perfect diamagnets with very large diamagnetic susceptibility. Even the best-known diamagnets (which are non-superconductors) have magnetic susceptibilities of the order of 10−5. Thus, the diamagnetic property can be considered a distinct property of superconductors compared to zero electrical resistance.

The near-complete expulsion of the magnetic field from a superconducting specimen is called the Meissner effect

A typical experiment demonstrating the Meissner effect can be thought of as follows: Take a superconducting sample (T < Tc), sprinkle iron filings around the sample, and switch on the magnetic field. The iron filings are going to line up in concentric circles around the specimen. This implies the expulsion of the flux lines outside the sample, which makes the filings line up.

Distinction between perfect conductors and superconductors

The distinction between a perfect conductor and a superconductor is brought about by magnetic field-cooled (FC) and zero-field-cooled (ZFc) cases, as shown below in Fig. 1.

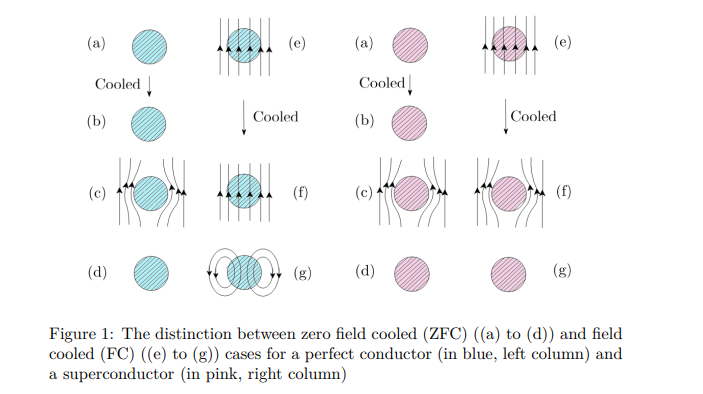
In the absence of an external magnetic field, temperature is lowered for both the metal and the superconductor in their metallic states from T > Tc to T < Tc (see left panel for both in Fig. 1). Hence, a magnetic field is applied, which eventually gets expelled owing to the Meissner effect. The field has finally been withdrawn. However, if cooling is done in the presence of an external field, after the field is withdrawn, the flux lines get trapped for a perfect conductor; however, the superconductor is left with no memory of an applied field, a situation similar to what happens in the zero-field cooling case. So, superconductors have no memory, while perfect conductors have memory.

Microscopic considerations: BCS theory

The first microscopic theory of superconductivity was proposed by Berdeen, Cooper, and Schrieffer (BCS) in 1957, which earned them a Nobel Prize in 1972. The underlying assumption was that an attractive interaction between the electrons is possible, which is mediated via phonons. Thus, electrons form bound pairs under certain conditions, such as (i) two electrons in the vicinity of the filled Fermi Sea within an energy range ¯hωD (set by the phonons or lattice). (ii) The presence of phonons or the underlying lattice is confirmed by the isotope effect experiment, which confirms that the transition temperature is proportional to the mass of ions. Since the Debye frequency depends on the ionic mass, it implies that the lattice must be involved. 3 A small calculation yields that an attractive interaction is possible in a narrow range of energy. This attractive interaction causes the system to be unstable, and a long-range order develops via symmetry breaking. In a book by one of the discoverers, namely, Schrieffer, he described an analogy between a dancing floor comprising couples, dancing one with any other couple, and being completely oblivious to any other couple present in the room. The couples, while dancing, drift from one end of the room to another but do not collide with each other. This implies less dissipation in the transport of a superconductor. The BCS theory explained most of the features of the superconductors known at that time, such as (i) the discontinuity of the specific heat at the transition temperature, Tc. (ii) Involvement of the lattice via the isotope effect. (iii) Estimation of Tc and the energy gap. The value of Tc and the gap are confirmed by tunnelling experiments across metal-superconductor (M-S) or metal-insulator-superconductor (MIS) types of junctions. Giaever was awarded the Nobel Prize in 1973 for his work on these experiments. (iv) The Meissner effect can be explained within a linear response regime. (v) Temperature dependence of the energy gap, confirming gradual vanishing, which confirms a second-order phase transition. Most of the features of conventional superconductors can be explained using BCS theory. Another salient feature of the theory is that it is non-perturbative. There is no small parameter in the problem. The calculations were done with a variational theory where the energy is minimised with respect to some free parameters of the variational wavefunction, known as the BCS wavefunction.

Unconventional Superconductors: High-T_c Cuprates

This is a class of superconductors where the two-dimensional copper oxide planes play the main role, and superconductivity occurs in these planes. Doping these planes with mobile carriers makes the system unstable towards superconducting correlations. At zero doping, the system is an antiferromagnetic insulator (see Fig. 2). With about 15% to 20% doping with foreign elements, such as strontium (Sr), etc. (for example, in La2−xSrxCuO4), the system turns superconductivity. There are two things that are surprising in this regard. (i) The proximity of the insulating state to the superconducting state; (ii) For the system initially in the superconducting state, as the temperature is raised, instead of going into a metallic state, it shows several unfamiliar features that are very unlike the known Fermi liquid characteristics. It is called a strange metal.

In fact, there are some signatures of pre-formed pairs in the ‘so-called’ metallic state, known as the pseudo gap phase. Since the starting point from which one should build a theory is missing, a complete understanding of the mechanism leading to the phenomenon cannot be understood. It remained a theoretical riddle.

Up Next

Scientists in India manipulate ‘non-conducting metal’ to pass electricity again

Don't Miss

A stellar encounter may have decided our climate

Dr. Saurabh Basu

Dr. Saurabh Basu is Professor at Department of Physics, Indian Institute of Technology (IIT) Guwahati. He works in the area of correlated electron systems with the main focus on bosonic superfluidity in (optical) lattices.

Click to comment

Space & Physics

Study Shows Single Qubit Can Outperform Classical Computers in Real-World Communication Tasks

This new research, however, offers compelling evidence of quantum systems’ power in a real-world scenario

Published

2 weeks ago

January 18, 2025

EP Staff

Image credit: Gerd Altmann /Pixabay

Breakthrough Study Shows Quantum Systems Can Outperform Classical Computers in Real-World Communication Tasks

A new study from the S. N. Bose National Centre for Basic Sciences in West Bengal, India, in collaboration with international teams has revealed that even the simplest quantum system, a single qubit, can surpass its classical counterpart in certain communication tasks. This discovery reshapes our understanding of quantum computing and hints at a future where quantum technologies could solve problems that classical computers, even with ample resources, cannot.

Quantum systems have long been seen as the next frontier in computing, with the potential to revolutionize technology. However, proving their superiority over classical systems has been a challenge, as experiments are complex, and limitations often arise that suggest quantum advantage might not be as accessible as once thought. This new research, however, offers compelling evidence of quantum systems’ power in a real-world scenario.

Professor Manik Banik and his team at the S. N. Bose Centre, alongside researchers from the Henan Key Laboratory of Quantum Information and Cryptography, Laboratoire d’Information Quantique, University libre de Bruxelles, and ICFO—the Barcelona Institute of Science and Technology, have demonstrated that a single qubit can outperform a classical bit in a communication task, even when no extra resources, like shared randomness, are available. The theoretical study, published in Quantum, was accompanied by an experimental demonstration featured as an Editors’ Suggestion in Physical Review Letters.

The team’s innovative approach involved developing a photonic quantum processor and a novel tool called a variational triangular polarimeter

The key to this breakthrough lies in the way quantum and classical systems handle communication. Classical communication often relies on shared resources, such as pre-agreed random numbers, to function efficiently. Without these shared resources, the task becomes more challenging. In contrast, the researchers found that a qubit does not require such help and can still outperform a classical bit under the same conditions.

The team’s innovative approach involved developing a photonic quantum processor and a novel tool called a variational triangular polarimeter. This device enabled them to measure light polarization with high precision using a technique known as Positive Operator-Valued Measurements (POVM). These measurements play a crucial role in understanding the behavior of quantum systems, particularly under realistic conditions that include noise.

“This result is particularly exciting because it demonstrates a tangible quantum advantage in a realistic communication scenario,” said Professor Banik. “For a long time, quantum advantage was mostly theoretical. Now, we’ve shown that even a single qubit can outperform classical systems, opening up new possibilities for quantum communication and computing.”

This research represents more than just an academic milestone; it brings us a step closer to a future where quantum technologies could drastically alter how we process and communicate information. As quantum systems continue to develop, this breakthrough makes the divide between quantum and classical computing not only more fascinating but also more attainable. The study also signals that quantum systems may eventually be able to solve problems that classical computers struggle with, even when resources are limited.

With this discovery, the potential for quantum communication and computation is moving from theoretical to practical applications, making the future of quantum technologies look even more promising.

Space & Physics

IIT Kanpur Unveils World’s First BCI-Based Robotic Hand Exoskeleton for Stroke Rehabilitation

The BCI-based robotic hand exoskeleton utilizes a unique closed-loop control system to actively engage the patient’s brain during therapy

Published

3 weeks ago

January 15, 2025

EP Staff

Image credit: By Special arrangement

The Indian Institute of Technology Kanpur (IITK) has unveiled the world’s first Brain-Computer Interface (BCI)-based Robotic Hand Exoskeleton, a groundbreaking innovation set to revolutionize stroke rehabilitation. This technology promises to accelerate recovery and improve patient outcomes by redefining post-stroke therapy. Developed over 15 years of rigorous research led by Prof. Ashish Dutta from IIT Kanpur’s Department of Mechanical Engineering, the project was supported by India’s Department of Science and Technology (DST), UK India Education and Research Initiative (UKIERI), and the Indian Council of Medical Research (ICMR).

The BCI-based robotic hand exoskeleton utilizes a unique closed-loop control system to actively engage the patient’s brain during therapy. It integrates three key components: a Brain-Computer Interface that captures EEG signals from the motor cortex to detect the patient’s intent to move, a robotic hand exoskeleton that assists with therapeutic hand movements, and software that synchronizes brain signals with the exoskeleton for real-time feedback. This coordination helps foster continuous brain engagement, leading to faster and more effective recovery.

“Stroke recovery is a long and often uncertain process. Our device bridges the gap between physical therapy, brain engagement, and visual feedback creating a closed-loop control system that activates brain plasticity, which is the brain’s ability to change its structure and function in response to stimuli,” said Prof. Ashish Dutta. “This is especially significant for patients whose recovery has plateaued, as it offers renewed hope for further improvement and regaining mobility. With promising results in both India and the UK, we are optimistic that this device will make a significant impact in the field of neurorehabilitation.”

Traditional stroke recovery often faces challenges, especially when motor impairments stem from damage to the motor cortex. Conventional physiotherapy methods may fall short due to limited brain involvement. The new device addresses this gap by linking brain activity with physical movement. During therapy, patients are guided on-screen to perform hand movements, such as opening or closing their fist, while EEG signals from the brain and EMG signals from the muscles are used to activate the robotic exoskeleton in an assist-as-required mode. This synchronization ensures the brain, muscles, and visual engagement work together, improving recovery outcomes.

Pilot clinical trials, conducted in collaboration with Regency Hospital in India and the University of Ulster in the UK, have yielded impressive results. Remarkably, eight patients—four in India and four in the UK—who had reached a recovery plateau one or two years post-stroke achieved full recovery through the BCI-based robotic therapy. The device’s active engagement of the brain during therapy has proven to lead to faster and more comprehensive recovery compared to traditional physiotherapy.

While stroke recovery is typically most effective within the first six to twelve months, this innovative device has demonstrated its ability to facilitate recovery even beyond this critical period. With large-scale clinical trials underway at Apollo Hospitals in India, the device is expected to be commercially available within three to five years, offering new hope for stroke patients worldwide.

Space & Physics

Obituary: R. Chidambaram, Eminent Physicist and Architect of India’s Nuclear Program

Rajagopala Chidambaram (1936–2025), a man whose work shaped the future of modern India, will always be remembered as the chief architect of India’s nuclear journey.

Published

1 month ago

January 4, 2025

EP Staff

Rajagopala Chidambaram, a world-class physicist and the chief architect of India’s nuclear program, passed away on January 4, 2025, at the age of 88. Renowned for his unparalleled contributions to India’s nuclear defense and energy security, Chidambaram leaves a profound legacy in both the scientific community and the nation’s strategic defense apparatus.

Born on November 11, 1936, in India, Dr. Chidambaram was an alumnus of Presidency College, Chennai, Tamil Nadu, and the Indian Institute of Science, Bengaluru, Karnataka. His academic background, coupled with his innate curiosity and vision, led him to become one of India’s foremost scientific minds. Throughout his illustrious career, Dr. Chidambaram played an instrumental role in shaping India’s nuclear capabilities, overseeing both the Pokhran-I (1974) and Pokhran-II (1998) nuclear tests, which cemented India’s position as a nuclear power on the world stage.

As a physicist, Dr. Chidambaram’s groundbreaking research in high-pressure physics, crystallography, and materials science greatly advanced the understanding of these fields. His pioneering work laid the foundation for modern materials science research in India, contributing to the nation’s scientific progress in multiple areas. His expertise in these complex disciplines not only bolstered India’s nuclear research but also advanced its technological prowess.

In addition to his work in nuclear weapons development, Dr. Chidambaram made significant strides in nuclear energy, ensuring that India remained at the forefront of scientific and technological advancements. As Director of the Bhabha Atomic Research Centre (BARC) and later as Chairman of the Atomic Energy Commission of India, he was integral to India’s peaceful nuclear energy initiatives. As Principal Scientific Adviser to the Government of India, Dr. Chidambaram guided national policies on defense, energy, and nuclear research, shaping the future of India’s scientific endeavors.

He was a vital member of the team that conducted India’s first nuclear test, Smiling Buddha, at Pokhran in 1974. His leadership during the Pokhran-II tests in 1998, which confirmed India’s nuclear deterrent, was a defining moment in the nation’s history. Chidambaram’s steadfast commitment to India’s defense and scientific advancement earned him respect both at home and abroad.

Rajagopala Chidambaram captured during the session ‘Innovative India’ at the Annual Meeting 2008 of the World Economic Forum in Davos, Switzerland. Copyright by World Economic Forum/Photo by Monika Flueckiger

A visionary leader, Dr. Chidambaram believed in the power of science and technology to drive national development. His efforts were instrumental in championing key initiatives in energy, healthcare, and strategic self-reliance. He steered numerous projects that significantly advanced India’s science and technology landscape. Notably, he played a central role in the indigenous development of supercomputers and was the driving force behind the conceptualization of the National Knowledge Network, which connected research and educational institutions across India.

Dr. Chidambaram was also an ardent advocate for the application of science and technology to improve societal conditions. He established the Rural Technology Action Groups and the Society for Electronic Transactions and Security, among other programs. His emphasis on “Coherent Synergy” in India’s scientific efforts helped foster collaboration across various disciplines, accelerating the country’s scientific growth.

On the global stage, Dr. Chidambaram served as the Chairman of the Board of Governors of the International Atomic Energy Agency (IAEA) in 1994-1995 and contributed to several high-level international nuclear discussions. His expertise was sought worldwide, and in 2008, he was appointed to the Commission of Eminent Persons by the IAEA to assess the agency’s role in nuclear governance.

He was a vital member of the team that conducted India’s first nuclear test, Smiling Buddha, at Pokhran in 1974

In recognition of his exceptional contributions to science and national development, Dr. Chidambaram received several prestigious accolades, including the Padma Shri in 1975 and the Padma Vibhushan in 1999. He was also awarded honorary doctorates from several universities and was a fellow of several eminent Indian and international scientific academies.

Dr. Chidambaram’s passing marks the end of an era for India’s nuclear program and the global scientific community. His legacy as a scientist, visionary leader, and architect of India’s nuclear journey will continue to inspire future generations. His contributions to national security, energy, and technological innovation have left an indelible mark on India’s scientific and strategic landscape.

Rajagopala Chidambaram’s profound impact on India’s nuclear and scientific trajectory will be remembered for generations to come. His work in advancing both national defense and the peaceful use of nuclear energy stands as a testament to his vision of a self-reliant, scientifically empowered India.

“Deeply saddened by the demise of Dr Rajagopala Chidambaram. He was one of the key architects of India’s nuclear programme and made ground-breaking contributions in strengthening India’s scientific and strategic capabilities. He will be remembered with gratitude by the whole nation and his efforts will inspire generations to come,” Prime Minister Narendra Modi wrote on X.

Dr. Ajit Kumar Mohanty, Secretary, Department of Atomic Energy, in a statement issued, said, “Dr. Chidambaram was a doyen of science and technology whose contributions furthered India’s nuclear prowess and strategic self-reliance. His loss is an irreparable one for the scientific community and the nation.”